数学I:数と式-整式編(例題つき)

はじめに
単項式・多項式
練習問題

はじめに

このページでは数学Ⅰの中でも最初の単元である｢数と式｣の中の整式に関する箇所について解説していきます。

単項式・多項式

単項式について

定義:単項式

単項式とは数や文字、またはそれらの積として表される式のこと。

単項式の定義は上記です。単項式という文字の通り1つの項だけからなる式のことですね。(これを単に項とも呼びます)例を見てみましょう。

例

・$ 2 $はただ1つの数なので単項式

・$ 5x $は$ 5 $という数と$ x $という文字の積で表されるので単項式

・$ 3 x^2 y^3 $ は　$ 3 \times x \times x \times y \times y \times y $ のように数と文字の積で表せるので単項式

・$ x + y $は文字と文字の和で表される(積では表せない)ので単項式ではない(→後述する多項式といいます)

このように積(かけ算)だけで表せるものを単項式といいます。足し算や引き算ではいけないのですね。

単項式の係数

単項式に文字が含まれているとき、その文字にかけられている数をその文字の係数といいます。

例

・$ 5x $の係数は$ 5 $

・$ 3 x^2 y^3 $ の係数は$ 3 $

・$ x $ の係数は$ 1 $(係数の$ 1 $は省略されることがほとんどなので注意)

・$ -x $ の係数は $ -1 $(マイナスまで含むことに注意)

・$ \frac{2x}{5} $の係数は$ \frac{2}{5} $ ( $ \frac{2x}{5} = \frac{2}{5}x $と書ける

単項式の次数と定数項

単項式に文字が含まれているとき、かけられている文字の数を単項式の次数といいます。

例

・$ 5x $の次数は$ 1 $

・$ 3 x^2 y^3 $ の次数は$ 5 $　( $ x $が2つと$ y $が3つかけられている)

・$ 4 $の次数は$ 0 $(→このように文字が1つもかけられていない単項式を定数項といいます)

次数が大きい/小さいを次数が高い/低いということもあります。

多項式について

定義:多項式

いくつかの単項式の和(足し算)で表される式を多項式という。

多項式の定義は上記です。多項式という文字通りいくつかの項からなる式のことですね。例を見てみましょう。(物によっては単項式も多項式に含むこともありますが、ここでは単純に項が1つのものを単項式、項が複数のものを多項式とします。)

例

・$ x + y $

・$ 6x^2 + 4x – 1 $

定義には単項式の足し算と書いてありますが例にはマイナスも出てきました。これはどういうことかというと、例えば2つ目の多項式は$ 6x^2 + 4x – 1 = (6x^2) + (4x) + (-1) $のように、$ 6x^2 $と$ 4x $と$ -1 $の3つの項の足し算として表せるからです。

注意

今後出てくるであろう$ \frac{1}{x} $ や $ \sqrt{x} $を含むものは文字の掛け算や足し算で表すことができないので単項式にも多項式にもなりません。

ここまでの単項式と多項式をあわせて整式と呼びます。

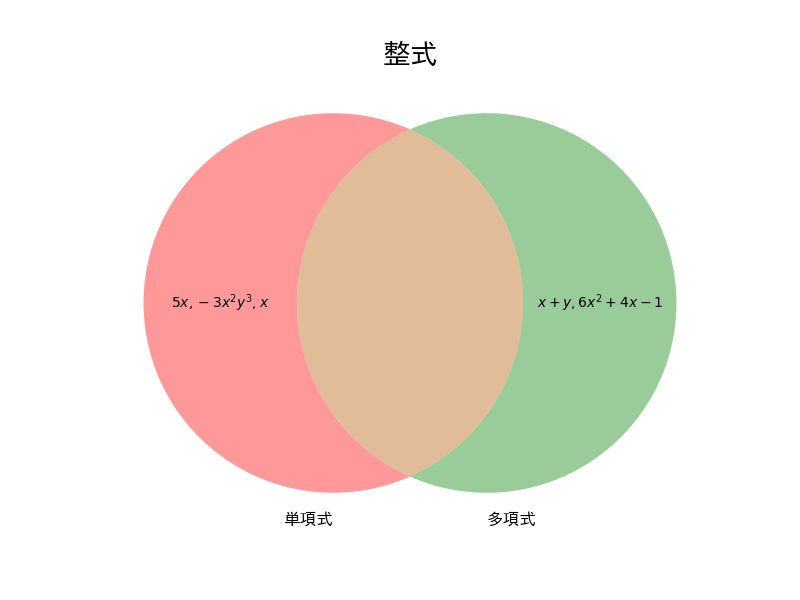
(↑実はこの図は少しおかしいです。ここでは単項式と多項式は別々(互いに排反)としているのでこれらの共通部分は存在しません。)

多項式の次数と定数項

多項式にも単項式と同じく次数が存在しますが、単項式と違って少し複雑なので注意して確認してください。

多項式における次数とは、多項式に含まれる項の中で、もっとも次数の高い項の次数のことを指します。よく分かりませんね。具体例を交えて説明します。以下の多項式を考えましょう。

$$ 2x^3 – 5x^2 + 4x – 6 $$

この多項式の次数は$ 3 $です。多項式に含まれるすべての項の次数を調べると、$ 2x^3 $の次数は$ 3 $、$ -5x^2 $の次数は$ 2 $、$ 4x $の次数は$ 1 $、$ -6 $の次数は$ 0 $なので1番大きい次数の$3 $が選ばれる訳です。

そして多項式を、その次数を使って◯次式と分類することもできます。(この場合は3次式)

また、多項式にも単項式と同じく定数項が存在します。これは単純に次数が$ 0 $の項を多項式の定数項と呼びます。(今回の場合は定数項は$ -6 $ )

さらに、多項式に含まれる項が次数の高い順に並んでいることを降べきの順といい、逆に次数の低い順に並んでいるを昇べきの順といいます。(言葉自体はほぼ出てきませんが、式の書き方としては降べきの順で書くことが基本です)

上記の多項式は降べきの順に並んでおり、これを昇べきの順で並べると以下のようになります。

$$ -6 + 4x – 5x^2 + 2x^3 $$

応用的な話

これまでの単項式、多項式に登場する文字はほとんど1種類でした。しかし今後、2種類以上の文字が登場することが多いのでその場合の扱い方を少し解説します。

文字が複数存在しているとき、その中で特に着目する文字を決めることがあります。次のような多項式を考えましょう。

$$ 3x^3y – 5x^2y^2 + x – 9 $$

この多項式には$ x $と$ y $の2種類の文字が含まれています。ここで$ x $という文字に着目するとき、この多項式は3次式であり、定数項は$ -9 $です。ある文字に着目するということは、それ以外の文字をただの数扱い(文字ではない)するということを意味します。ですので例えば第1項の係数は$ 3y $ になります。また上の多項式は着目している文字$ x $の次数が高い順に並んでいるので降べきの順であると言えます。

次に上の多項式で$ y $に着目してみます。このとき多項式を降べきの順で書き直すと以下のようになります。

$$ -5x^2y^2 + 3x^3y + x – 9 $$

このとき、この多項式は2次式であり、定数項は$ x – 9 $です。ここで勘の良い方はある違和感を覚えているかもしれません。先ほど、定数項とは次数が0の項(単項式)であると言いましたが、今回の定数項($ x – 9 $ )はこれまでの単項式には見えません。

これは$ x $という文字を、文字ではなく数として扱っているということが関係します。$ x $は$1$とか$7$のようなただ1つの数なので、$ x – 9 $もただ1つの数として扱えるはずです。したがって、$ x – 9 $ を単項式扱いするわけです。

最後に$ x $と$ y $の両方に着目してみます。この場合はどちらも文字として扱うので、多項式は4次式、定数項は$ -9 $となります。

練習問題

最後に練習問題を使ってここまでの内容を復習しましょう。

問題1

以下の式を単項式、多項式、またはそれ以外に分類せよ。

$$ 3, 0, 7x + 6, xy^2, \frac{3}{x + 2}, \frac{x + 2}{3}, x^2 – y^2 $$

解答

単項式:$ 3, 0, xy^2 $

多項式:$ \frac{x + 2}{3} (= \frac{1}{3}x + \frac{2}{3} $と書ける), $x^2 – y^2$

単項式、多項式以外: $ \frac{3}{x + 2} $

問題2

以下の単項式の係数と次数を答えよ。指定がある場合はその文字に着目すること。

$$ 2x $$

解答

係数:2,次数:1

$$ 7x^3 $$

解答

係数:7,次数:3

$$ 5xy^4 ( y に着目して) $$

解答

係数:$ 5x $,次数:4

問題3

以下の多項式の次数と定数項を答えよ。指定がある場合はその文字に着目すること。

$$ x + 6 $$

解答

次数:1,定数項:6

$$ 5x – x^2 + 2x^3 -1 $$

解答

次数:3,定数項:-1

$$ x^3y^2 + 9xy^3 – 7x^2y + x -1 　(xに着目して)$$

解答

次数:3、定数項:-1

$$ x^3y^2 + 9xy^3 – 7x^2y + x -1 　(yに着目して)$$

解答

次数:3,定数項:$ x – 1 $

$$ x^3y^2 + 9xy^3 – 7x^2y + x -1 　(x, yに着目して)$$

解答

次数:5,定数項:-1